Noise Floor on Synaptic Weight
When it comes time to upload any brain, C. elegans, D. melanogaster, or H. sapien, the process will not be perfect. Connections will be missed and synaptic weight will not be measured accurately. The question is, how will that error propagate to the actual ethology of the uploaded mind? In this post I will present my crude first steps to answering that question.
Ok enough with the semi-pseudo-academic talk, I want to know how good of an upload is good enough. In general, I want to know if error is roughly linear or exponentially. What does that mean? If all the weights in your brain were randomly changed by 10% of their current value would you perform within 10% of your current score on an IQ test? If so, then the error propagations is roughly linear. If instead it scales exponentially your performance might be something like 0.9^(1E14) which may as well be 0. Obviously this is a very contrived example leaving out a lot of mathematical nuance and all the possible constants and other functions that could inform how this error propagates but I think it gets the point across.
It would also be useful to know what noise how noise tolerant synaptic weight in in an absolute sense, not just how it scales. Maybe it scales linearly but there is a coeffeicent such that even a 1% error leads to catastrophic brain damage or other radical behavioral change.
I'm just going to get ahead of it now, this post will not give definitive answers for these questions, even in the small model systems I'm using here and certainly not for a human brain. That said, I do genuinely think this is a useful avenue of research. Even outside the context of WBE, humans do not seem susceptible to adversarial attacks the way current AI is so investigating how noise exists in the system may be a way to prevent such attacks. Or it may be completely useless, I'm not a ML guy and I don't care to be. It was an idle though I had though so why not throw it out there? As another aside, my limited understanding of neuroscience makes me think that there is essentially no timescale on which synaptic weight in a real biological system is constant. What do I mean by that? There is essential a random variance in the excitation of a post-synaptic neuron given a pre-synaptic neuron firing. Sometimes no action potential is transmitted, sometimes the neurotransmitter is depleted in that particular synapse, whatever. Bottom line is that thinking of a single definite synaptic weight that gets updated in accordance to some learning rule the way modern ML works is, in my opinion, not a super accurate way of looking at real brains. Now that I've got you hopes down, I'll start in on some of the technical details.
I used both snnTorch (second link to docs) and then just normal pytorch to train a total of 4 neural networks, 2 spiking and 2 "traditional". They were trained on the MNIST digit classification dataset and then also this Alzheimer's dataset. Not a real good reason for picking either, they were just easier to work with. I'm not going to go into the details of snnTorch, in no small part because I don't know all of them, but it uses leaky integrate and fire neurons and works with surrogate back propagation training. You can't do real backpropagation on spikes because they are inherently discontinuities but you can fake it and get good results. That said, this isn't biologically plausible which is why I spent all that time trying, and failing so far, to get good results with a rule I consider to be biologically plausible. At some point I will need to revisit this with better learning rules or maybe even one of the models of C. elegans but right now I'm putting a pin in this to work on some other stuff.
So what do I actually do to see the effect of a noisy/imperfect upload? For noise, I looked at the standard deviation of the weights in each particular layer, then I generated gaussian random noise for each weight in that layer with mean of 0 and standard deviation being a multiple of the natural standard deviation in that given layer. Now, the distribution of weights was not naturally gaussian and was different in different layers so this may be objectionable for a few reasons, but I think it is a good first pass and a somewhat realistic way that weights may be misread when uploading. As for dropout, that is easier. Some fraction of the synaptic weights were just set to 0 for a given run. In a real upload, connections may be spuriously added but it is unclear to me how I would realistically model that. I have a few ideas but they all seem like they would take a lot of work and not yield much insight so I have forwent them for the time being (All glory to the time being).
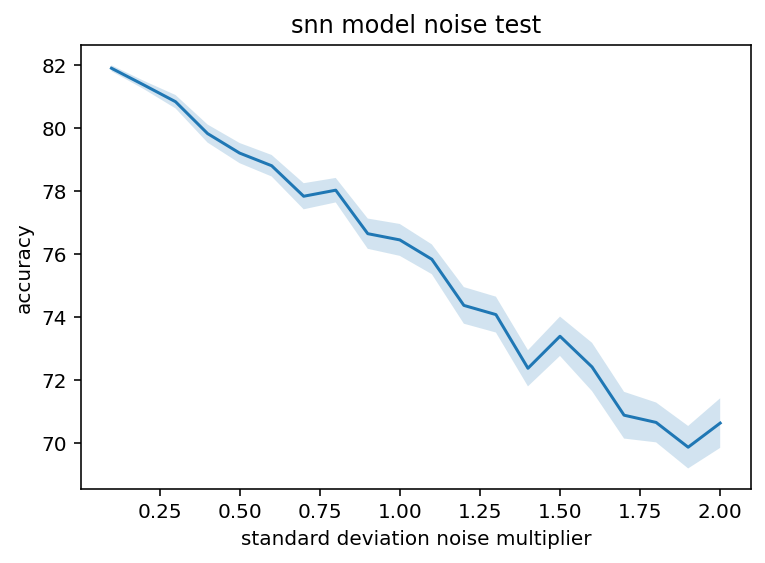
And here are the actual results. First up we have the noise and dropout of the spiking neural network of MNIST classification:
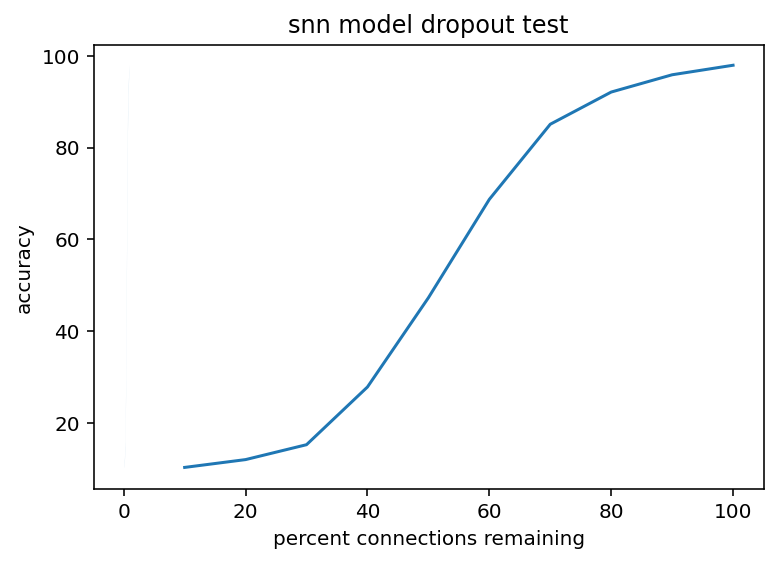
The light bands around the noise line are the SEM, tested with 50 different random noise values
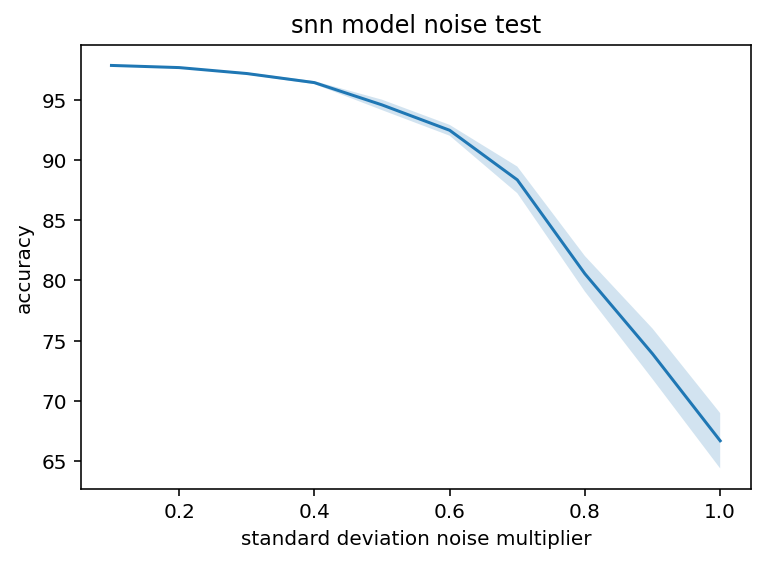
As you can see, peak accuracy is around 97%. This is actually perhaps the best possible shape. We know there is going to be some performance degradation but this like less than linear if that makes sense. Accuracy can be modeled as A*(1-x)^n where n < 1 in this case which is great. Now, the absolute value is a little concerning but hey, it is directionally good and getting 0.1 standard deviations away from the true value sounds like an achievable goal. As for dropout, it is pretty encouraging which is not super surprising, it is kind of a sigmoid in this case and, again, there is not a precipitous drop for all values other than being completely perfect which is what we want. Below are the same charts for a traditional neural network.
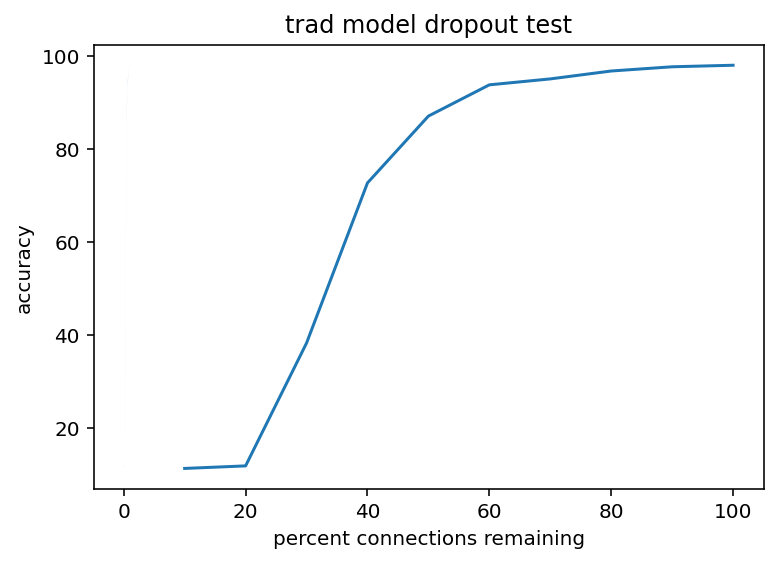
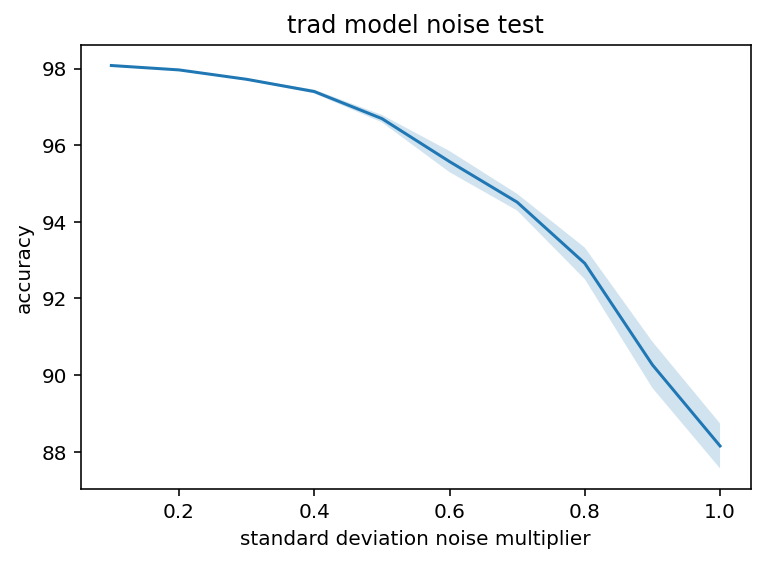
As you can see these are very similarly shaped although there are some differences. For starters, the dropout seems to be less sigmoid-ish, more of a step increase after 20% dropout. That hardly matters, whatever we do better be in the upper 90s for percent of true connections. Also interestingly, the traditional model seems to be much more robust to noise addition. I'm not sure exactly what causes this and it's sufficiently far away from my real goals I'm not going to investigate but it is counter to my expectations. Spiking networks are so inherently noisy I just assumed that noise in the weights would be absorbed into that and make a smaller difference but I was evidently wrong, at least in this case.
And here are all the same graphs for the Alzheimer's dataset. The overall accuracy was much lower but I am more concerned with relative performance.
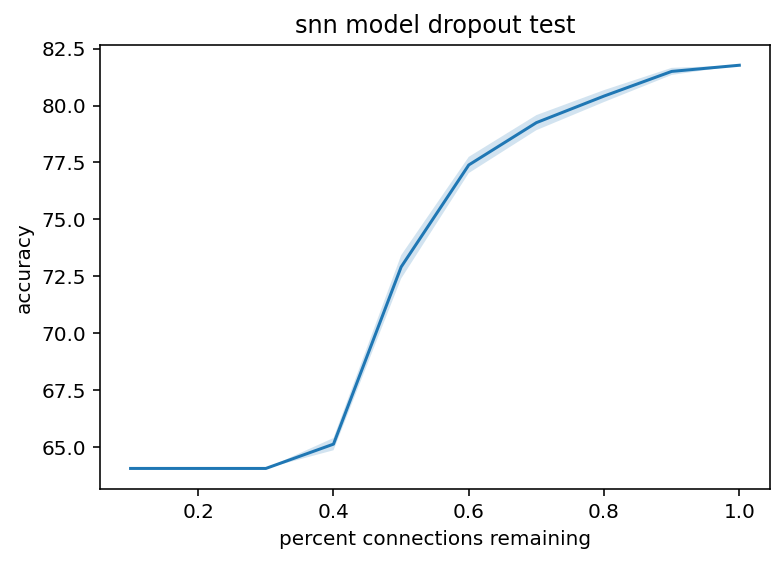
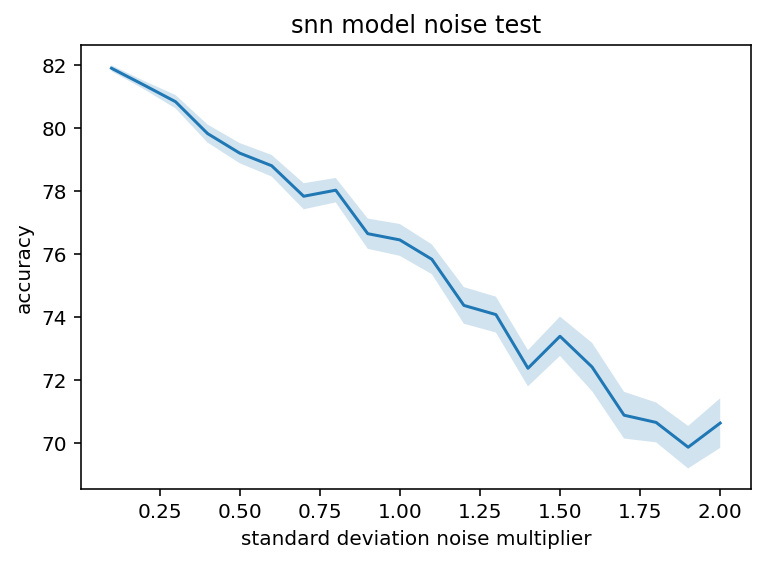
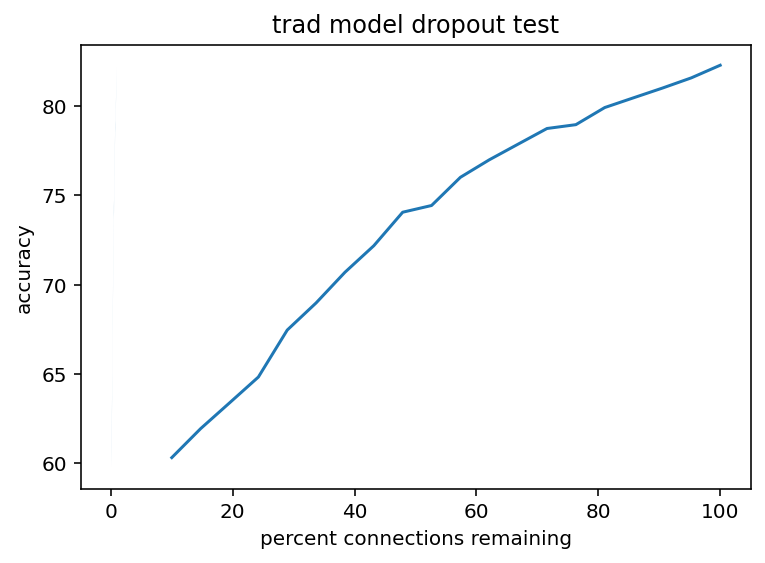
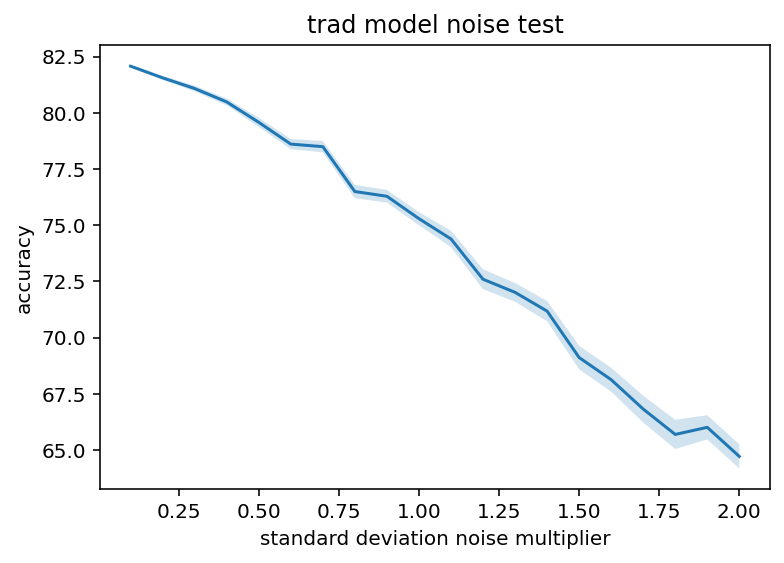
These graphs are slightly different shapes but I think not in anyway that is really meaningfully. I mean the noise additions are much more linear which opens the door to the possibility that some architectures/trained models might have that dreaded exponential error issue but I still haven't seen it so without further testing it's just a black swan I guess.
In conclusion, there is a lot more I could do but probably won't for a while. I am satisfied taking away the information that
- there are no ugly discontinuities with low noise and it almost certainly does not scale with a "bad" exponential (i.e. 99% accurate synaptic weights will get you in the neighborhood of 99% similar performance)
- dropout does not cause problems at the scale in which humans can check an automated systems work, humans will never map a human connectome manually but we can make sure an automated system is 99% accurate by manually tracing small regions ourself.
I guess in retrospect this is kind of the obvious or default answer, still good to check and I guess it is still necessary to see how this scales to larger/more complex systems.
This does bring up the interesting philosophical question of how close is close enough to be you? I have no answer and I can't really imagine we live in a world where the answer to that kind of question is going to make me give up on the idea of chasing/advocating for some kind of radical life extension. Still cool to ponder.
As always, here is the code.